Current Components in a Transistor in Active Region Operation

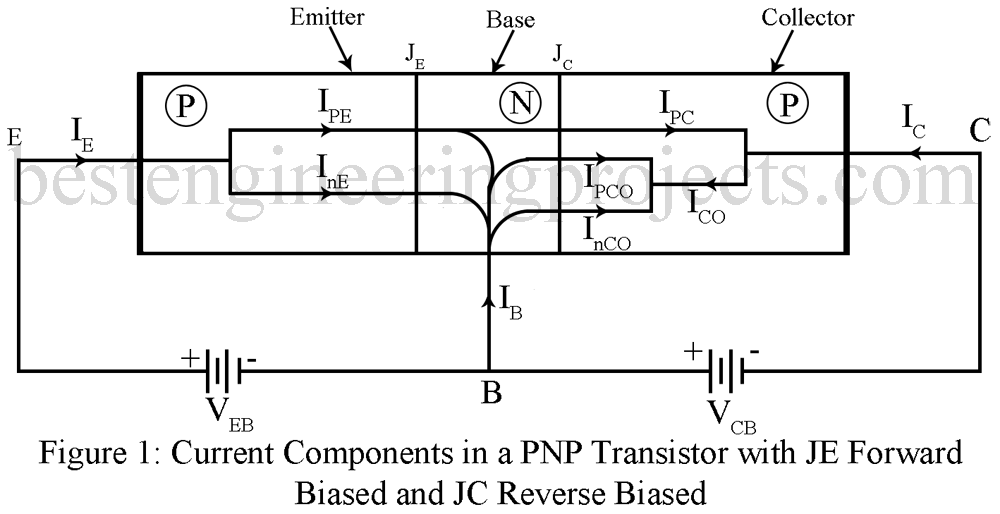
Figure 1 shows the various current components in a pnp transistor operating in the active region. The entire emitter current I_E consist of two parts (i) hole current I_pE carried by holes diffusing across J_E from p-type emitter to n-type base and (ii) electron current I_nE carried by electrons diffusion across J_E from n-type base to p-type emitter. The ratio $\dfrac{I_{pE}}{I_{nE}}$ equals $\dfrac{\sigma_{pE}}{\sigma_{nB}}$ where $\sigma_{pE}$ and $\sigma_{nB}$ are respectively the conductivity of the p-type emitter region and n-type base region. Typically $\sigma_{pE}$ > $\sigma_{nB}$ . Hence in a pnp transistor, I_pE>>I_nr and hence we may neglect I_nE. This forms a desirable feature since the current component I_nE does not contribute charge carriers which ultimately reach the collector.

Forward bias at J_E results in injection of holes across J_E into the base region. These minority holes diffuse through the base constituting the hole diffusion current I_pE.This current is proportional to the slope of the hole density p_n at K_E. Hence this current I_pE is given by,

$I_{pE} = -qD_p A\dfrac{d_{pn}}{dx}$ ………..(1)

Where D_p is the diffusion constant for holes and A is the cross-sectional area.

Similarly, I_nE is proportional to the electron density n_p at J_E and is given by,

$I_{pE} = -qD_n A\dfrac{d_{pn}}{dx}$ …………….(2)

Where, D_n is the diffusion constant for electrons.

Total emitter current I_E crossing J_E is the sum of I_pE and I_nE. Thus,

$I_E = I_{pE} + I_{nE}$ …………(3)

All these currents I_E, I_pE and I_nE are positive in a pnp transistor.

The holes while diffusion through n-type base region, meet majority carrier electrons ad some of these holes recombine with electrons giving rise to a small base current. The hole current I_pc on reaching the collector is, therefore, slightly less than I_pE. The holes on reaching J_C across it easily (since they travel down the potential barrier) and enter the p-type collector region. Since, the width of the base region is very small, almost all the holes injected into the base reach the collector junction and get collected by the p-type collector.

In addition to current I_pC, there is another current at J_C namely reverse saturation current I_CO (or I_CBO). This I_CO is sum of two components: (i) current I_nco caused by electrons diffused across J_C from n-type collector to n-type base and (ii) current I_PCO caused by holes diffusion across J_C from n-type base to p-type collector. Hence, we have,

$-I_{CO}=I_{nco} + I_{pco}$ ……….(4)

In equation 4, minus sign has been added to I_CO intentionally so that I_C and I_CO may have the same assigned direction of flow.

I_PCO results exclusively from the holes generated thermally within the base while I_nco results from the electrons generated thermally within the collector.

Under the active region operation with J_E forward biased, the collector current is given by,

$I_C = I_{CO}-I_{pC}$ …….(5)

$= I_{CO}-\alpha I_E$ ……..(6)

Where $\alpha$ is the fraction of the total current I_E which constitutes I_pC.

In a pnp transistor, I_e is positive while both I_Cand I_COare negative since the current in the collector lead actually flows in the direction opposite to that indicated by the arrow on I_C in figure 1.

Total diffusion hole current across J_C from the base into the collector is,

$I_{pct} = I_{pC} + I_{pCO}$ …………(7)

Large Signal Current Gain $\alpha$

The term $\alpha$ has already been defined above. However, equation 6 permits us to define $\alpha$ in an alternative manner. Thus, from equation 6, $\alpha$ may be defined as the ratio of collector current increment from cutoff value (I_C = I_CO) to the emitter current increment from cutoff (I_E = 0). Thus, we may write,

$a = -\dfrac{(I_C-I_{CO})}{(I_E-0)}$ ………..(8)

Term $\alpha$ is called the large signal current gain of a common base transistor. I_C and I_E have opposite signs in both pnp and npn transistors. Hence, $\alpha$ as defined by equation 8 is always positive. Typically $\alpha$ lies in the range 0.90 to 0.995. Further $\alpha$ is not constant. It varies with emitter current I_E, collector voltage V_CB and the temperature.

DC Current gain $\alpha_{dc}$

If I_CO<I_C then from equation 8, $\alpha$ approximately equals $\dfrac{I_C}{I_E}$ . This is referred to as the dc current gain of CB transistor and is denoted by $\alpha_{dc}$ .

Thus, $\alpha_{dc} = -\dfrac{I_C}{I_E}$ ………..(9)

Quantity $\alpha_{dc}$ is also always positive and less than unity.

Small Signal Current Gain $\alpha^1$

It is defined as,

$\alpha^1 = \dfrac{\Delta I_C}{\Delta I_E}| V_CB$ ………(10)

Where $\Delta I_C$ and $\Delta I_E$ are small changes in I_C and I_E.

Increments $\Delta I_C$ and $\Delta I_E$ have opposite signs. Hence $\alpha^1$ as defined by equation 10 comes out to be positive number. Further $\alpha^1$ is always less than unity but very close to it. Quantitate $\alpha^1$ also varies with I_E, V_CB and temperature.

Generalized Expression for Collector Current

Equation 6 giving I_C in terms of I_CO, $\alpha$ and I_E is valid for operation in the active region. Thus, for active region operation, I_C is almost independent of the collector voltage but depends only on the emitter current I_E. we now processed to obtain a generalized expression for I_C which is valid not only for reverse bias J_C but for any voltage across J_C.In that case, we need replace I_CO by the current in J_C acting as a pn diode i.e. $I_{CO}(1-\varepsilon^{\dfrac{V_C}{V_T}})$ where V_c is the voltage drop across J_C from p-side to n-side and V_T is the volt equivalent of temperature. Then from equation 6 we get the following generalized expression for I_C.

$I_C = -\alpha I_E + I_{CO}(1-\varepsilon^{\dfrac{V_C}{V_T}})$ …….(11)

If V_Cis negative and large in magnitude compared to V_T, Equation 11 reduce to equation 6.

Physical meaning of equation 11 is that the current in J_c (acting as a pn diode) gets supplemented by a fraction of I_E coming from the emitter.

Example 1: In a PNP transistor in CB configuration, only 0.5% of the holes injected into the base through J_E recombine with electrons in the base. If $20\times 10^8$ electrons leave the emitter in $1\mu s$ , how many enter the same lead and how many enter the collector lead during the same period.

Solution:

Number of electrons combining with holes in the base region per $\mu s = 0.005 \times 2 \times 10^8 = 10^6$ . Hence, 10⁶ electrons per $\mu s$ enter the base lead.

Hence, the number of electrons entering the collector leads per $\mu s = 2\times 10^8-10^6 = 199\times 10^6$ .

Example 2: In a PNP transistor operating in the active region in CB configuration. The collector current equals 9mA and the emitter current equals 9.2mA. Calculate the value of $\alpha$ and base current I_B. Neglect I_CO.

Solution:

$\alpha = -\dfrac{(I_C-I_{CO})}{I_E} \approx -\dfrac{I_C}{I_E} = \dfrac{9mA}{9.2mA} = 0.978$ $I_B = -(I_C + I_E) = -(-9 + 9.2) = -0.2 mA$

Example 3: In a PNP CB Transistor operating in the active region, the emitter current I_E = 8mA and $\alpha = 0.95$ . Calculate the collector current I_C and the base current I_B. Neglect I_CO.

Solution:

$\alpha = -\dfrac{I_C-I_{CO}}{I_E} \approx -\dfrac{I_C}{I_E}$

Hence, $I_C = -\alpha I_E = -0.95 \times 8mA = -7.6 mA$

Hence, $I_B = -(I_E + I_C) = -(8-7.6)mA = -0.4mA$

Example 4: In a PNP CB transistor operating in the active region, collector current I_C = -5mA and the base current $I_B = -100\mu A$ . Compute $\alpha$ of the transistor and the emitter current I_E.

Solution:

$I_E = -(I_C + I_B) = -(-5-0.1)mA = 5.1 mA$ $\alpha = -\dfrac{(I_C -I_{CO})}{I_E} \approx -\dfrac{I_C}{I_E} = -\dfrac{(-5mA)}{+5.1mA} = 0.98$

Example 5: In a PNP CB transistor operating in the active region, the emitter current I_E = 4mA, $I_{CO} = -4\mu A$ and $\alpha = 0.99$ . Calculate current and the base current.